Variantă a problemei precedente, rezolvată prin metoda eforturilor

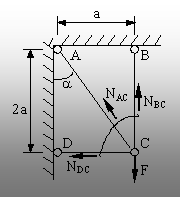
Fig. 5.23.

Se consideră un sistem de trei bare, identice ca material şi secţiune transversală, articulate la capete şi prinse în nodul comun C, în care acţionează forţa concentrată verticală F (fig. 5.23). Se cere să se determine forţa maximă pe care o poate prelua sistemul, dacă se cunoaşte că barele au secţiuni circulare, cu diametrul d=20mm, parametrul a=0,5m, iar rezistenţa admisibilă a materialului lor este s_a=150MPa.

Suplimentar, se cere să se calculeze deplasarea pe direcţie verticală a punctului C, în urma aplicării forţei, dacă materialul barelor are modulul de elasticitate E=2,1×10⁵ MPa

Rezolvare

Necunoscutele problemei sunt eforturile din bare (N_i – notate cu indicii nodurilor pe care le unesc), toate de direcţie axială, care se pun în evidenţă prin secţionarea imaginară a barelor, în jurul nodului comun, ca în figură.

Atenţie: Se face convenţia de a se reprezenta cu sensul de îndepărtare de nodul comun eforturile de întindere din bare! Dacă toate necunoscutele se vor marca în acest sens, rezultă că barele pentru care se vor obţine eforturi negative vor fi solicitate la compresiune.

Pe de altă parte, singurele ecuaţii de echilibru semnificative ale acestei probleme sunt cele două ecuaţii de proiecţii de forţe scrise pentru nodul comun C, sub forma:

(5.71)

Este necesară rezolvarea unui sistem de două ecuaţii cu trei necunoscute, adică problema este simplu static nedeterminată.