A. Rezolvarea nedeterminării

Se alege efortul (N_AC) drept necunoscută static nedeterminată a problemei, în funcţie de care se vor exprima celelalte două, pe baza sistemului (5.71) şi a valorilor funcţiilor trigonometrice ale unghiului a (calculate din triunghiul dreptunghic ACD):

Din ecuaţiile (5.71) se ajunge la:

(5.72)

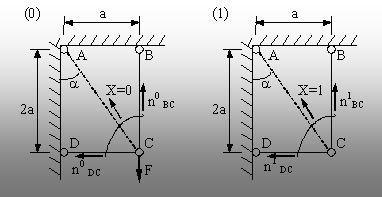
Aplicarea metodei presupune transformarea sistemului dat într-unul static determinat, numit sistem de bază (în care se îndepărtează bara care conţine necunoscuta static nedeterminată şi se face substituţia N_AC=X), pentru care se vor studia două stări fictive de solicitare (fig. 5.24), astfel:

Fig. 5.24.

· Starea “0” – cu bara oblică întreruptă (deci nesolicitată, X=0) şi cu forţa exterioară F prezentă.

· Starea “1” – fără forţa F, dar cu efort egal cu o unitate (X=1) în bara oblică.

Atenţie: Spre deosebire de alte cazuri de aplicare a metodei eforturilor, aici bara pe care se aplică efortul de o unitate trebuie să fie adăugată sistemului de bază, în starea “i" de solicitare. Pentru ca necunoscuta (X_i) să aibă valoarea 1, este nevoie ca bara căreia îi corespunde să existe în sistem!

Pentru cele două stări de solicitare se scriu ecuaţiile de echilibru, de tipul (5.71), sub forma:

(5.73)

Ecuaţia metodei eforturilor se scrie sub forma:

(5.74)

iar coeficienţii (d) se calculează cu relaţii de tipul (5.38), astfel:

respectiv:

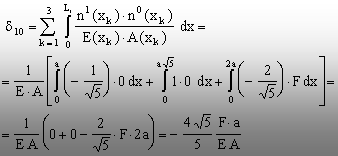
Pe baza acestor valori, ecuaţia (5.74) conduce la aflarea necunoscutei X:

iar din sistemul (5.72) se obţin celelalte două eforturi secţionale:

Atenţie: Calculul numeric al eforturilor va putea fi făcut numai după aflarea valorii admise a forţei F, care este una dintre cerinţele problemei!