C. Calculul deplasării pe verticală a punctului în care se aplică forţa F

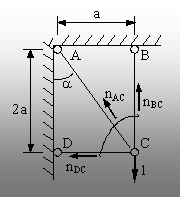
Fig. 5.25.

Sistemul îndeplineşte condiţiile pentru aplicarea metodei Mohr - Maxwell, pe baza unei relaţii de calcul de tipul (5.37), pentru calculul deplasării cerute. În acest scop, se eliberează (imaginar) sistemul de solicitarea exterioară (fig. 5.25), iar în punctul C se introduce o forţă concentrată de mărime egală cu o unitate (abstractă, deci fără dimensiuni), având direcţia deplasării căutate.

Pentru determinarea eforturilor fictive (n_i) din bare, este nevoie de rezolvarea unei noi probleme static nedeterminate.

Această rezolvare devine imediată, dacă se observă similitudinea perfectă a stării de solicitare din figura 5.25 cu aceea din figura 5.23, pentru care valorile necunoscutelor s-au găsit la punctul A de mai sus.

Prin urmare, se poate spune direct că:

n _AC = 0,443; n _CD = -0,198; n _BC = 0,604

Aceste eforturi sunt mărimi adimensionale, deoarece reprezintă fracţiuni din forţa fictivă 1. Aplicarea relaţiei (5.37) va conduce la determinarea deplasării cerute:

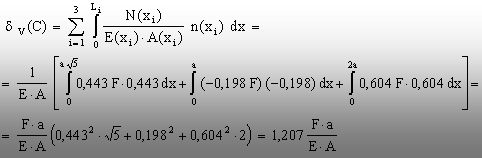
Folosind datele numerice ale problemei, inclusiv forţa maximă calculată mai sus, se obţine:

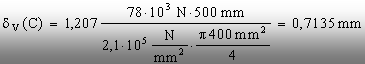
Observaţii

1. Deplasarea calculată mai sus este a punctului C, deoarece acolo a fost aşezată forţa fictivă unitară şi este pe direcţie verticală – deoarece forţa egală cu 1 a avut această direcţie.

2. Dacă s-ar dori să se afle deplasarea totală a lui C, atunci trebuie făcut un calcul similar celui de mai sus, pentru deplasarea pe orizontală d_H(C) (deci cu forţă unitară orizontală în C).

Acest calcul implică rezolvarea unei probleme simplu static nedeterminate, cu totul similară primului paragraf din problema de faţă. Deplasarea lui C va fi: