Tensiuni şi deformaţii specifice

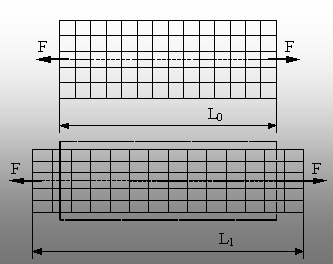
Fig. 5.1. Analiza deformării prin tracţiune

a unei bare prismatice.

Se consideră o bară prismatică, pe a cărei suprafaţă se trasează o reţea de linii, longitu-dinale şi transversale, ochiurile reţelei fiind pătrate.

Dacă se aplică, la capetele barei, două forţe egale şi contrare (fig. 5.1), atunci bara este solicitată la tracţi-une, iar dacă se anali-zează forma pe care o ia bara după solicitare se observă că:

Þ Bara se alungeşte cu cantitatea DL = L₁–L₀

Þ Se produce şi o contracţie transversală, astfel încât pătratele iniţiale ale reţelei de linii se transformă în dreptunghiuri, alungite pe direcţia solicitării. Rezultă că în bară apar numai tensiuni de tip axial (s) şi se produc numai deformaţii specifice liniare (e).

Þ Secţiunile care erau iniţial plane şi perpendiculare pe axa barei îşi păstrează aceste caracteristici după producerea solicitării, chiar dacă se deplasează de-a lungul axei, adică se respectă în mod riguros ipoteza lui Bernoulli.

Se poate deci spune că, cel puţin în domeniul deformării elastice şi proporţionale cu forţa aplicată, deformarea se produce în mod uniform în întregul volum al unei zone de secţiune constantă şi cu încărcare constantă pe lungimea ei (L), de pe o bară solicitată axial. Această condiţie poate fi exprimată matematic sub forma:

(5.1)

Pe de altă parte, având în vedere presupunerea că nu se depăşeşte, prin solicitare, limita de proporţionalitate a materialului, rezultă că este respectată legea lui Hooke, adică se poate scrie că:

(5.2)

Prin urmare, solicitarea de tracţiune produce, într-o bară de tipul precizat, o distribuţie uniformă a tensiunilor şi deformaţiilor specifice, adică o stare omogenă de tensiuni şi deformaţii. Este singura solicitare simplă care prezintă această caracteristică, ceea ce explică importanţa acordată încercării la tracţiune a materialelor, precum şi multitudinea de concluzii rezultate din efectuarea ei.