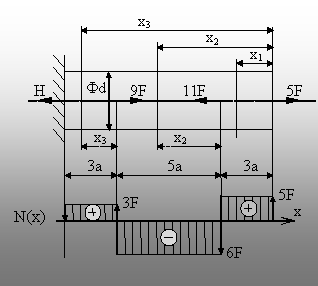
Exemplu: 5.1. Să se traseze diagrama de efort pentru bara din figura 5.2.

Notă După cum se obişnuieşte în rezolvarea problemelor de rezistenţa materialelor, aici şi în continuare mărimile care figurează în enunţul aplicaţiilor – încărcări, lungimi, dimensiuni de secţiune – se vor exprima, atunci când este posibil, sub formă literală, depinzând de un parametru precizat. Acest fapt uşurează înţelegerea fenomenelor fizice care însoţesc solicitările studiate şi permite generalizarea rezolvărilor.

Fig. 5.2. Trasarea unei diagrame de efort axial.

Construirea diagramelor de eforturi este precedată de analiza solicitării barei, în conformitate cu regulile prezentate în capitolele anterioare.

Astfel, bara de faţă, având lungimea L=11a, este încastrată la capătul din stânga şi liberă la celălalt (bară în consolă), iar încărcarea este formată din trei forţe concentrate de direcţie axială.

Singurul tip de efort interior este forţa axială, astfel că, pe de o parte, în reazem apare o singură reacţiune nenulă – forţa H, iar pe de altă parte se poate scrie o singură ecuaţie de echilibru semnificativă (din care va rezulta valoarea reacţiunii, problema fiind static determinată) – aceea a proiecţiilor pe axa longitudinală a tuturor forţelor existente pe bară.

Se va putea deci scrie că: H = 5F - 11F + 9F <=> H = 3F

După cum se observă, studiul efortului axial trebuie făcut pentru trei regiuni ale barei, delimitate de punctele în care se aplică forţele exterioare.

Secţiunile de calcul alese pe aceste regiuni vor fi marcate prin distanţa lor (x_i) faţă de un reper oarecare din planul desenului. Sunt indicate două variante (cele mai utilizate) ale acestei marcări:

· cu aceeaşi origine a coordonatei (x) (într-un capăt al barei) pentru toate regiunile – cotarea din partea de sus a figurii 5.2;

cu origine proprie fiecărei regiuni (preferată, de obicei, a se afla chiar la capătul regiunii precedente) – cotarea din partea de jos, cu linii punctate.

Observaţii

1. Spre deosebire de calculele matematice, în rezistenţa materialelor sensul de parcurgere a barei (sensul axei x de pe diferite regiuni) nu are impor-tanţă, deoarece semnificaţia fenomenelor se păstrează şi dacă acest sens este către stânga. Axa (x) marcată pe diagramele de eforturi este pur simbolică, amintind că se studiază variaţia solicitărilor pe lungimea barei.

2. Modul cum se alege originea lui x de pe o anumită regiune se reflectă în exprimarea lungimii respectivei regiuni. Astfel, cea de-a doua zonă de studiu de pe bara propusă (fig. 5.2) este intervalul [3a; 8a], pentru originea lui (x₂) aşezată în capătul din dreapta al barei, dar va fi intervalul [0; 5a] – dacă originea se plasează în capătul primei regiuni, (varianta de cotare din partea de jos a desenului).

Trecând la determinarea expresiilor analitice (care sunt, în acest caz, foarte simple) ale efortului axial de pe cele trei regiuni ale barei studiate, se va ţine seama de cele prezentate anterior cu privire la definirea lui N(x), respectiv la convenţia de semne (sunt pozitive forţele care supun la tracţiune secţiunea de calcul). Se obţin următoarele rezultate (regiunile se scriu cu originea lui x în capătul barei):

Pentru x₁ = (0; 3a)

· dacă se urmăresc forţele situate în partea dreaptă faţă de secţiunea

de calcul N(x₁) = 5F = ct.

· dacă se sumează forţele din stânga N(x₁) = H – 9F + 11F = 5F = ct.

În conformitate cu definiţia eforturilor interioare, cele două variante de calcul duc la acelaşi rezultat, dar în aplicaţiile concrete se va alege, evident, varianta pentru care calculele sunt mai simple.

Pentru x₂ = (3a; 8a) N(x₂) = 5F – 11F = –6F = ct.

Pentru x₃ = (8a; 11a) N(x₃) = 5F – 11F + 9F = 3F = ct.

Rezultă că efortul axial este constant pe fiecare dintre cele trei intervale de definiţie, iar graficul său, adică diagrama de efort, se prezintă în figura 5.2.

Se remarcă prezenţa celor patru puncte de discontinuitate (“salturi”) de la graniţele regiunilor. Posibilitatea apariţiei acestor discontinuităţi ale diagramelor impune prezentarea intervalelor de definiţie ca deschise (prin paranteze rotunde).

Concluzii asupra trasării diagramelor de efort axial:

1. Dacă asupra barei nu acţionează încărcări distribuite, atunci efortul este constant pe lungimea fiecărei regiuni.

2. În punctele de aplicare a forţelor concentrate se produc salturi în diagramă, care coincid ca mărime şi sens cu forţele respective. De exemplu, în punctul de graniţă dintre primele două regiuni apare un salt, de la (+5F) la (-6F), având adică mărimea de (11F) şi sensul negativ, aşa cum este (conform convenţiei făcute) forţa concentrată din acel punct al barei.

Aceste observaţii îşi vor păstra valabilitatea şi la studiul celorlalte eforturi secţionale