Exemple de calcul

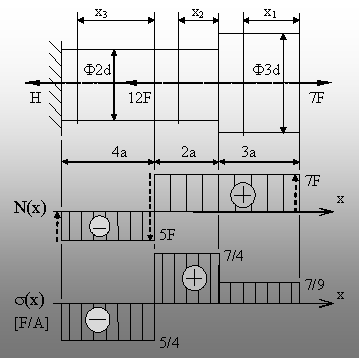
5.2. Se consideră o bară cilindrică în consolă, formată din două tronsoane de diametre şi lungimi diferite şi solicitată prin două forţe concentrate, de direcţie axială (fig. 5.3).

Fig. 5.3.

Notă: În vederea efectuării calculelor de rezistenţă, indi-ferent de natura solicitării din bara studiată, este nevoie să se stabilească variaţia eforturilor secţionale, respectiv a tensiunilor, pe lungimea barei, adică trebuie să se traseze diagrama de efort - în acest caz N(x), respectiv diagrama tensiunilor (sau a tensiunilor maxime)- aici s(x).

Pentru a se păstra posibilitatea de generalizare a rezolvării, toate calculele privitoare la aceste diagrame se vor face literal, urmând ca datele numerice să fie introduse în exemplificarea propriu-zisă a calculului de rezistenţă.

Pe de altă parte, se recomandă a se urmări treptat explicaţiile privind trasarea celor două diagrame, făcându-se abstracţie de faptul că diagramele sunt deja prezentate, în partea de jos a figurii 5.3.

Rezolvare

După cum se observă, punctele de aplicare a forţelor delimitează pe bară numai două regiuni, dar saltul de secţiune de la interfaţa tronsoanelor conduce la apariţia celei de-a treia.

Se alege varianta de măsurare a variabilei x de la capătul din dreapta al fiecărei regiuni, aşa cum se arată în figură.

Deoarece bara este solicitată numai axial, se observă că în încastrare există un singur tip de reacţiune, forţa H, iar singura ecuaţie de echilibru semnificativă se scrie:

H + 12F – 7F = 0

de unde rezultă că H = –5F. Acest rezultat arată că reacţiunea are, de fapt, semn contrar forţei 12F.

Se trece la stabilirea parametrilor solicitării, pe regiuni, aşa cum se arată în continuare.

Pentru x₁Î(0; 3a) efortul axial este N(x₁) = 7F = ct.

Aria secţiunii transversale

Se preferă a se simplifica scrierea, prin notaţia ,

de unde rezultă că A(x₁) = 9A.

Tensiunile de pe prima regiune vor fi:

După cum se observă, toate cele trei mărimi care apar în aceste calcule au fost exprimate în funcţie de anumiţi parametri literali, ceea ce va permite compararea valorilor lor de pe regiuni diferite.

Pentru cea de-a doua regiune, cu x₂Î(0; 2a), se obţin următoarele rezultate:

N(x₂) = 7F = ct.

În fine, pentru x₃Î(0; 4a), valorile sunt:

N(x₃) = 7F – 12F = –5F = ct. A(x₃) = 4 A

Folosind aceste rezultate, se trece la trasarea diagramelor, după cum se explică în cele de mai jos.

Diagrama de efort axial N(x)

· Pe bară există două zone distincte – una de întindere, sub forţa 7F, cealaltă de compresiune, cu forţa interioară 5F.

· Graficul prezintă trei puncte de discontinuitate (salturi – indicate pe desen prin săgeţi cu linii punctate), care coincid ca punct de apariţie, mărime şi sens cu forţele concentrate de pe bară.

· Saltul din dreptul reazemului confirmă valoarea reacţiunii H, precum şi sensul ei, acelaşi cu al forţei 7F, din capătul liber al barei.

Se poate observa că, în problemele de acest tip, reacţiunea poate fi determinată direct, din diagrama de efort, fără a se mai scrie ecuaţia de echilibru, deci făcând rezolvarea mai rapidă.

Pe de altă parte, trebuie subliniat faptul că simpla cunoaştere a efortului din secţiunile transversale ale barei nu este suficientă pentru a se evidenţia solicitarea maximă din piesă. Aceasta va fi determinată de aria secţiunii pe care se distribuie efortul, adică de valoarea tensiunii din bară.

Diagrama tensiunii s(x)

· Acest grafic conţine trei zone distincte, care coincid cu regiunile de pe bară. Punctele de discontinuitate sunt determinate de modificarea valorilor N(x) şi A(x), deci salturile nu mai au o semnificaţie fizică.

· Intensitatea solicitării este perfect vizibilă pe această diagramă. Secţiunea periculoasă (în care bara se poate distruge, dacă parametrii barei sau ai încărcărilor sunt aleşi incorect) poate fi oricare dintre secţiunile transversale de pe regiunea de mijloc a barei, de lungime (2a).

· Calculele de rezistenţă se vor baza pe o relaţie de forma (5.5), astfel:

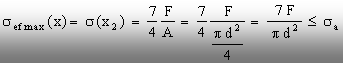(5.8)

Observaţii

1. Este interesant de subliniat că în această relaţie nu apare parametrul a, deci calculele de rezistenţă nu sunt influenţate de lungimea barei.

2. Pe de altă parte, în legătură cu zona de pe bară solicitată la compresiune, pot fi întâlnite două situaţii de calcul:

a) Materialul barei are valori diferite ale rezistenţei admisibile la întindere (s_{a tract}) şi compresiune (s_{a comp}), deci se scrie o relaţie de forma (5.8) pentru compararea valorii absolute a tensiunii maxime de compresiune din bară cu (s_{a comp}).

b) Materialul are aceeaşi rezistenţă admisibilă la tracţiune şi compresiune, deci este suficientă scrierea unei singure relaţii de forma (5.8), pe baza valorii maxime, în modul, a tensiunii efective din piesă.

Exemplificarea calculelor de rezistenţă se va face prin trei serii distincte de date numerice.

A. Verificare

Presupunem că se cunosc F=2×10⁴N, d=15mm, s_a=150MPa.

Pentru a adeveri corectitudinea realizării barei, se introduc aceste date în membrul stâng al inecuaţiei (5.8):

Se observă că valoarea maximă a solicitării depăşeşte (cu peste 30%) rezistenţa admisibilă a materialului barei, situaţie care nu poate fi acceptată. Prin urmare, se pot lua două feluri de măsuri:

Þ Mărirea ariei secţiunii transversale a barei – de exemplu prin creşterea diametrului la valoarea d=20mm. Repetând calculul de mai sus, se obţine s_{ef max}(x) = 111,38MPa valoare corectă.

Alegerea unui material cu rezistenţa la tracţiune mai mare decât 198MPa, ceea ce face ca sensul inegalităţii (5.8) să fie cel corect.

B. Determinarea forţei capabile

Se dau: d=20mm, s_a=150MPa.

Pe baza formulei (5.8), se scrie o relaţie de forma membrului stâng al inecuaţiei (5.6), astfel:

Rezultă că valoarea parametrului F nu poate depăşi, în acest caz, 2,7×10⁴N.

C. Dimensionare

Se cere să se determine valoarea necesară a parametrului d, dacă F=2×10⁴N şi s_a=150MPa.

Din inecuaţia (5.8) rezultă că:

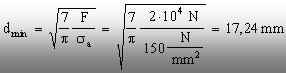
Pe această bază se adoptă o valoare convenabilă a lui d, cum ar fi d_ad=18mm. Această valoare se va utiliza în toate calculele ulterioare din problema respectivă