Calcule bazate pe criteriul de rigiditate

Pentru calculul deformaţiilor şi deplasărilor în barele solicitate axial, pe baza legii lui Hooke şi a definiţiilor (anterioare ale) tensiunilor (s) şi deformaţiilor specifice (e), se poate scrie că:

(5.9)

Regulă de calcul

Deplasarea unei secţiuni arbitrare (x) este determinată numai de deformarea părţii de bară situată între acea secţiune şi capătul fixat al barei (sau unul dintre capete, dacă ambele sunt fixate). Prin urmare, această deplasare se calculează ca sumă algebrică a deformaţiilor tronsoanelor incluse în respectiva porţiune de bară.

Consecinţe

1. Dacă pe un tronson al barei se menţin constante mărimile N(x)=N şi A(x)=A, atunci deformaţia totală a lui, adică deplasarea reciprocă a capetelor tronsonului se va scrie:

(5.10)

2. Dacă pe o regiune (de lungime L) a barei se produc variaţii (după funcţii anumite, de variabilă x) ale celor două mărimi, atunci deplasarea secţiunii arbitrare (x) de pe acea regiune, în raport cu originea considerată a lui x, se calculează cu relaţia:

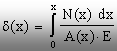(5.11)

3. După cum rezultă din relaţia (5.11), în cazul în care mărimea ariei A(x) este constantă pe porţiuni ale barei (adică variază în trepte pe lungimea ei), atunci gradul funcţiei deplasărilor d(x) este cu o unitate mai mare decât al funcţiei N(x). Faptul este important, întrucât uşurează studiul şi trasarea diagramei deplasărilor d(x), în problemele în care se impune acest lucru.

4. Dacă tema de proiectare precizează anumite valori limită (admisibile) pentru deformaţiile absolute (Dl) sau cele relative (e) ale piesei, atunci sunt necesare calcule similare celor de rezistenţă, bazate însă pe criteriul de rigiditate şi care pot fi:

a) de verificare

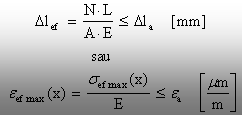(5.12)

b) de forţă capabilă

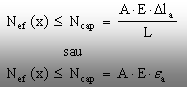(5.13)

c) de dimensionare

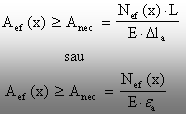(5.14)

5. Produsul (E×A) este denumit rigiditatea (sau modulul de rigiditate) la tracţiune (şi compresiune) a barei studiate.