Exemplu de calcul

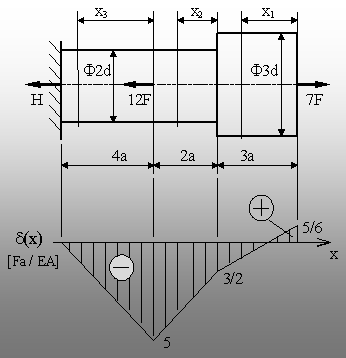
5.3. Se propune a se relua în atenţie bara din figura 5.3, pentru a se analiza modul în care se modifică poziţia secţiunilor transversale ale barei, în urma solicitării discutate mai sus.

Rezolvare

Bara fiind solicitată numai axial, rezultă că secţiunile ei se vor deplasa, la stânga sau la dreapta, faţă de poziţia lor în bara lipsită de încărcări.

Dacă se ţine seama de studiul făcut anterior asupra barei rezultă, pe baza consecinţelor 1 şi 3 de mai sus, că:

Þ deformaţia absolută a celor trei tronsoane de bară se calculează cu câte o relaţie de forma (5.10);

Þ funcţia deplasărilor d(x) are gradul cu o unitate mai mare decât al funcţiei N(x), deci va fi o funcţie de gradul întâi (liniară);

Þ întrucât nu interesează atât expresia analitică a acestei funcţii, cât valorile (deci graficul) ei, este suficient să se calculeze aceste valori pentru secţiunile de capăt ale celor trei regiuni de pe bară, iar graficul se va obţine prin unirea, cu segmente de dreaptă, a acestor trei puncte.

Fig. 5.4.

Pe de altă parte, este clar că unul dintre puncte se cunoaşte de la început: capătul prins în reazem al barei nu se poate de-plasa, deci graficul va începe de la valoarea zero. Studiul se va continua, pe baza re-gulii de calcul de mai sus, prin parcurgerea imaginară a barei, din reazem către capătul liber.

Păstrând convenţia de a exprima toate mări-mile în funcţie de anu-miţi parametri literali, deplasările capetelor dinspre dreapta ale celor trei tronsoane de bară, calculate cu relaţii de forma (5.10), vor fi următoarele:

Cu aceste valori a fost trasată diagrama deplasărilor d(x) (fig. 5.4). Se poate observa că semnele acestora sunt determinate de cele ale eforturilor axiale, (deplasările pozitive se produc în sensul forţelor considerate pozitive). Prin urmare, secţiunile cu valori pozitive se deplasează la dreapta, iar celelalte la stânga. Deplasarea maximă se produce în secţiunea de la capătul tronsonului de lângă reazem şi are semn negativ.

Ca exemplu numeric, să presupunem, preluând datele de la ultima aplicaţie anterioară, că se cunosc F=2×10⁴N ; E=2,1×10⁵ MPa ; a=0,1m şi d=18mm.

Dacă se propune a se determina valoarea (absolută) maximă a deplasării secţiunilor transversale, înlocuirea datelor numerice în expresia valorii extreme din diagramă conduce la următorul rezultat:

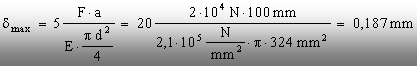(5.15)

Luând în considerare criteriul de rigiditate, se propune a se determina forţa maximă ce poate fi aplicată barei, astfel ca deplasarea maximă a oricărei secţiuni transversale să nu depăşească valoarea admisibilă d_a=0,1 mm.

Se introduce prima egalitate din relaţia (5.15) în membrul stâng al unei inecuaţii de forma (5.12). Se obţine valoarea limită admisibilă a parametrului F, sub forma următoare:

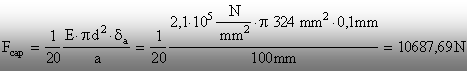
Prin urmare se poate admite că, pentru ca bara să respecte parametrul de deformabilitate impus, valoarea efectivă a parametrului F nu trebuie să depăşească limita de 10⁴N.