Calculul la strivire

În cazul unei solicitări de compresiune care se aplică pe suprafaţa de contact dintre două corpuri, este necesar să se evite distrugerea celor două suprafeţe prin fenomenul de strivire. În această situaţie, calculul de rezistenţă se bazează pe limitarea presiunii efective de contact, valoarea limită impusă fiind presiunea admisibilă a celui mai puţin rezistent dintre cele două materiale, după relaţia:

(5.16)

Fenomenul se produce, în mod tipic, în cazul tablelor îmbinate prin nituri sau şuruburi, iar un caz special de calcul este legat de contactul, pe suprafeţe semi-cilindrice, dintre table şi aceste elemente de îmbinare.

Un exemplu similar este contactul de tip rolă-sabot (fig. 5.5), caz în care echilibrarea forţei active F se realizează prin forţele distribuite uniform

p(a) = p_{ef str} = ct.

Fig. 5.5. Calculul ariei de strivire în cazul contactelor pe suprafeţe cilindrice.

Suprafaţa de contact, de formă semi-cilindrică, are mărimea

Considerând că forţele distribuite sunt dirijate normal la suprafaţa de contact, adică pe direcţie radială, echilibrul forţelor, proiectate pe direcţia verticală, se concretizează în următoarea ecuaţie:

(5.17)

în care factorul p(a) este constant, astfel că se scoate în afara integralei.

Dacă se notează cu (ds) elementul de arc de pe conturul secţiunii transversale a rolei, atunci aria elementară din integrala de mai sus va fi:

dA = g × ds = g × r da = g × (d/2) da

iar aria de strivire “de calcul” se determină din relaţia (5.17), astfel:

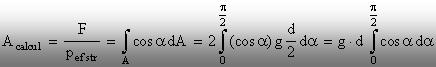(5.18)

Cum integrala care a rămas de calculat are valoarea 1, rezultă că se ia în considerare aria A_calcul = g×d. Aceasta este egală cu secţiunea “longitudinală” (diametrală) a porţiunii din piesa cilindrică pe care se produce contactul (aria vizibilă a rolei în secţiunea A-A din desenul de mai sus).

Observaţie importantă:

Contactul real nu conduce la apariţia unei presiuni uniforme între cele două piese (întrucât de cele mai multe ori au loc concentrări de tensiuni) şi nici la dirijarea pe direcţii strict radiale a componentelor p(a). Calculul prezentat este însă “acoperitor”, deoarece se ia în considerare o arie efectivă de contact mai mică (aproximativ cu 30%) decât aceea ideală (g×d < p×g×d/2).