A. Cazul aplicării statice a forţelor

Dacă o bară cu solicitare axială, aşezată în poziţie verticală, are greutatea proprie de mărime comparabilă cu forţele exterioare care produc solicitarea, atunci efectul greutăţii barei nu poate fi neglijat în calculele ei de rezistenţă şi de rigiditate.

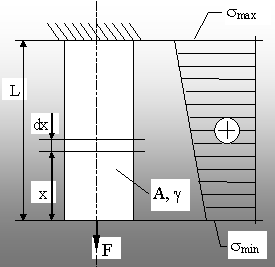
Fig. 5.7. Solicitarea la tracţiune a unei bare verticale cu greutate proprie mare.

Pentru bara din figura 5.7, se consideră cunoscute aria (A) a secţiunilor transversale şi greutatea unităţii de volum – (g) (greutatea specifică), astfel că efortul axial din secţiunea (x) a barei va fi:

N(x) = F + g A x

iar valoarea tensiunii efective este:

(5.21)

Tensiunile variază, pe înălţimea barei, după o funcţie de gradul întâi, ca în figura alăturată.

Valorile extreme ale tensiunile sunt:

şi (5.22)

Inegalitatea de la sfârşitul expresiei (5.22) reprezintă relaţia pe baza căreia se face calculul de rezistenţă pentru această bară. Prin urmare, dacă se doreşte dimensionarea barei, atunci din inegalitatea citată rezultă că:

(5.23)

Analizând numitorul acestei fracţii se poate observa că, pe măsură ce produsul (g×L), dintre greutatea specifică a materialului şi lungimea barei, se apropie de valoarea rezistenţei admisibile (s_a), aria secţiunii transversale trebuie să crească foarte mult.

În plus, se poate defini, pentru un material oarecare, mărimea (L_r) a lungimii unei bare care se va rupe sub solicitarea produsă numai de propria ei greutate. Această lungime se calculează pe baza rezistenţei la rupere a materialului respectiv, care trebuie să fie egalată de produsul (g×L).

Prin urmare, lungimea de rupere sub greutatea proprie este o altă mărime specifică fiecărui material şi care se calculează cu relaţia

(5.24)

Exemplu: pentru un oţel OL37, având rezistenţa la tracţiune s_r = 370 MPa şi greutatea specifică g = 78 kN/m³ se obţine lungimea de rupere

Rezultă o lungime foarte mare, dar care totuşi poate fi întâlnită în aplicaţiile din anumite domenii ale tehnicii, aşa cum sunt, de exemplu, utilajele de foraj la adâncimi mari.

Pentru calculul alungirii unei bare de tipul descris mai sus, se scrie mai întâi alungirea elementului de lungime elementară (dx) (fig. 5.7):

(5.25)

Ca urmare, alungirea totală a barei se va calcula astfel:

(5.26)

Se observă similitudinea dintre această relaţie şi expresia (5.10), de la alungirea unei bare solicitate la tracţiune doar de forţa F.

Consecinţe:

1. Deformaţia totală a unui tronson de bară cu greutate proprie mare se calculează la fel ca pentru barele de greutate neglijabilă adăugându-se, în cadrul termenului reprezentând forţa axială care solicită tronsonul, jumătate din greutatea proprie a tronsonului respectiv.

Cea de-a doua egalitate din şirul de egalităţi (5.26) arată că expresia analitică a deformaţiei (DL) are gradul cu o unitate mai mare decât expresia s(x), adică diagrama deplasărilor secţiunilor transversale d(x) va avea formă parabolică (cu valoarea maximă la capătul liber al barei).