B. Cazul aplicării dinamice a încărcării

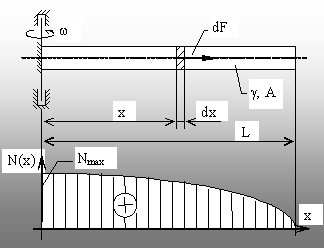
Fig. 5.8. Solicitarea axială prin forţe de inerţie.

Această situaţie apare în cazul forţelor de inerţie având direcţia axei barei, de exemplu la o bară care se roteşte cu viteza un-ghiulară (w), în planul ei longitudinal, în jurul unu-ia dintre capete, prins într-un reazem încastrat (fig. 5.8). Secţiunile piesei vor fi solicitate de forţele centrifuge din par-tea de corp situată către capătul liber.

Dacă se consideră cunoscute greutatea specifică (g), acceleraţia gravitaţională (g) şi aria (A) a secţiunii transversale a barei, atunci forţa centrifugă elementară se calculează cu relaţia:

Ca urmare, efortul axial din secţiunea arbitrară (x) va fi

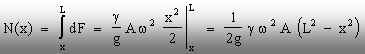(5.27)

Derivata întâi a acestei funcţii parabolice este o funcţie de gradul întâi, fără termen liber. Aceasta se anulează, prin urmare, în punctul x=0, în care funcţia N(x) va avea un extrem. În plus, derivata a doua a funcţiei este negativă, N’’(x)<0, de unde rezultă că punctul de extrem este un maxim relativ al funcţiei considerate.

Se observă că valorile funcţiei la capetele intervalului de definiţie sunt următoarele:

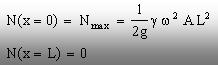(5.28)

Diagrama eforturilor axiale se prezintă ca în figura (5.8), iar secţiunea periculoasă a barei, având în vedere că secţiunea transversală are mărime constantă pe întreaga lungime, va fi aceea din capătul prins în reazem. Ca atare, calculul de rezistenţă se va face pe baza relaţiei:

(5.29)

Din ultima inecuaţie se poate cere să se calculeze, de exemplu, lungimea maximă admisibilă L_max a barei considerate. În alte cazuri s-ar putea cere (ştiind că viteza unghiulară şi turaţia sunt legate prin relaţia w=p n/30) stabilirea valorii maxime n_max a turaţiei cu care poate fi rotită, în condiţii de siguranţă, o bară pentru care se cunosc celelalte mărimi care sunt cuprinse în relaţia de mai sus.